简介

米勒定律指的是：在短时记忆中，人平均只能记忆7 (±2) 个项目。

这一法则强调了我们在处理信息时的认知限制，特别是在涉及记忆和理解信息时。设计师和沟通者可以利用米勒定律的原则，将信息组织成小的、易于理解的单元，以提高人们对信息的理解和记忆。

详情

1956 年，哈多大学的认知学教授 George A. Miller 发表了一篇名为《神奇数字7》的论文，该论文是人们关于短时记忆内容最早期的研究结果。该文章讨论了一维绝对判断 (绝对二进一决策) 的极限和短期记忆极限之间的巧合：一维绝对判断的备选数目与短期记忆极限的数目大致相当，数字都在 7 左右徘徊。 后来的研究虽然对 Miller 论文中的某一些概念进行了修正和完善，但是数字 7 却被保留了下来，成为了 UI/UX 设计中的一条经典普适的定律：米勒定律。

米勒定律可以应用在每一个需要排列项目组的地方，就比如我们常常能在 UI 设计中遇到这么一些问题：为什么是这个数字？为什么最多只能这么多？为什么分页组件的选项从来没有一次展示超过 7 项的？为什么功能入口一行最多只有 5 个？为什么 iOS 官方建议的 Tabbar 项目最多只有 5 个？我可以一直这么问下去。

I. 审视每一种需要排列的选项组

我们需要去控制每一个可能涉及选择的区域，所包含的选项数量不超过 9 个。

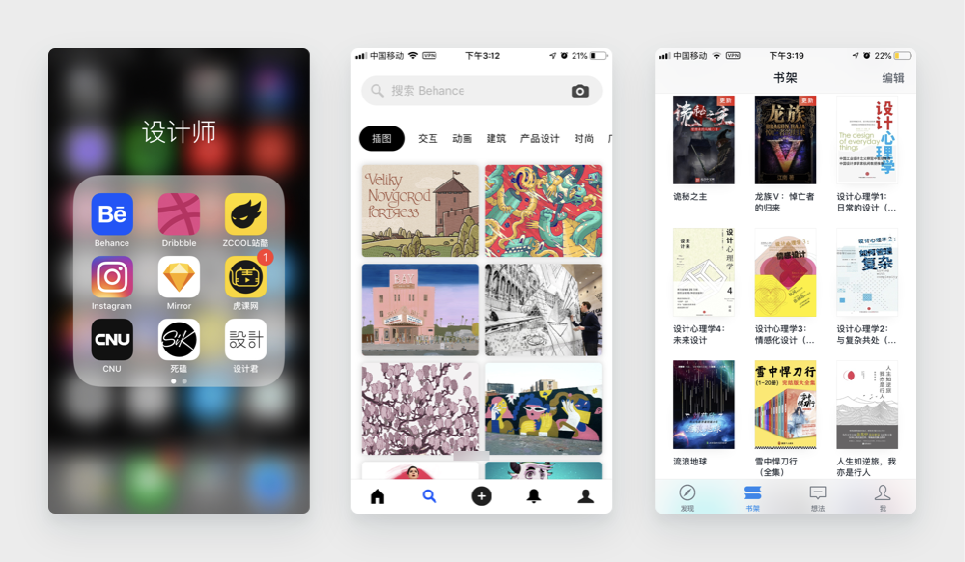
无论是 iOS 的应用文件夹一页最多只能展示 9 个应用 (缩略图也是) ，还是 behance 分页组件一次最多出现 7 个分页，还是微信读书书架页每一屏最多 9 本书，设计师在进行设计时都在时刻注意着米勒定律的影响。

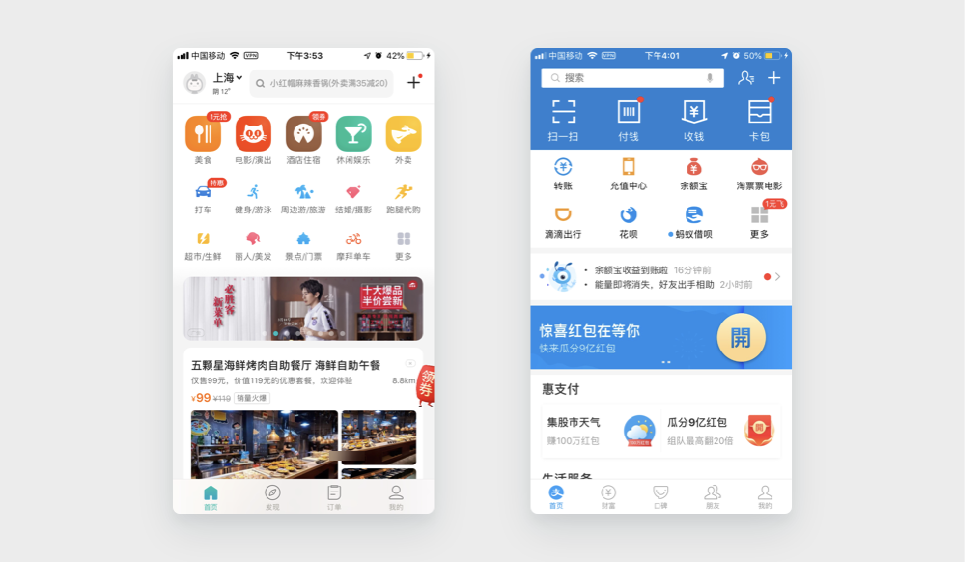
那么为什么有些应用的功能入口一组能有 10 个呢？尤其是京东、闲鱼、口碑、美团、网易严选这种体量大、分类又细又多的应用，功能入口超过 10 个轻轻松松。

它们的功能入口的的确确一次出现了 10 个，这仅仅是为了照顾强迫症患者吗？

仔细观察一下第二排最后一个，「分类」、「全部」、「超级会员」，是不是看起来和其他不太一样？它们没有其余 9 个有那么强的功能性和可选性，简单来说，它们看起来与其他选项是同级的、功能类似的，实则并不是，所以会与其他选项区分开来，它们就是在照顾强迫症患者 (以及视觉需求) ，正好方便把一些推广性的、或者用户不常用的、或者全部分类这样的功能点塞进去。

II. 选项的描述词也需要注意

选项越复杂，记忆跨度 (所能记忆的项目数量极限) 就会相应减少，这意味着选项一旦多起来，其描述词务必做到简单易懂、清晰可见。那些复杂的、自创的、不常见的、模糊的、自以为用户能懂的或看都看不清的描述词会增大用户记忆和理解难度，所以描述词的选取也值得每一位设计师去注意。

III. 利用希克定律和格式塔原理进行缩减和分组

这就又回到了如何控制选项数量与对选项分组的问题上来，参考之前所详细讲解过的希克定律和格式塔原理(邻近性、相似性、连通性、同域)，我们能够有效地对大量选项进行分类和分组，并对每一组进行更精确的数量控制，从而满足米勒定律的记忆要求。

IV. 信息同样需要分块处理

除了选项分组之外，有些信息也需要分块呈现。

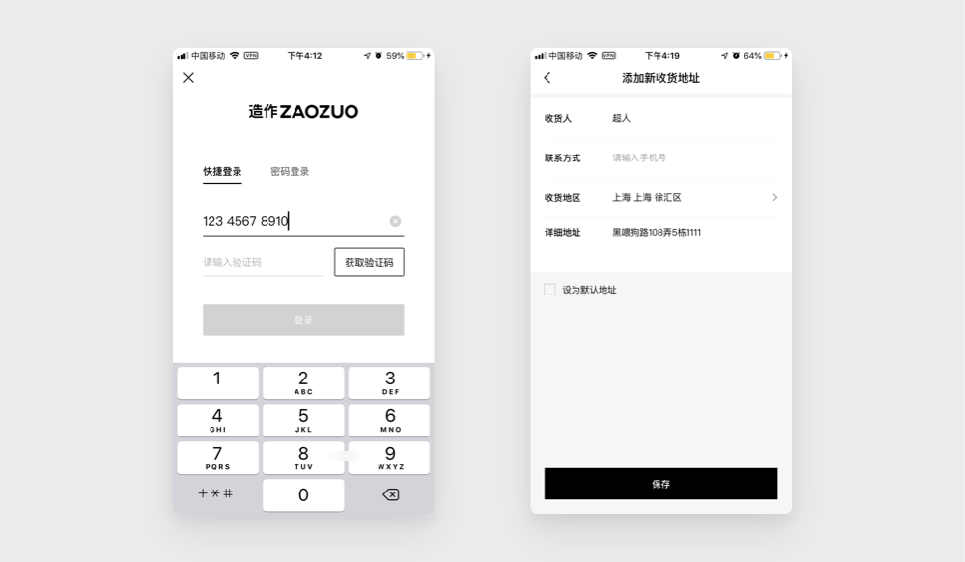
比如，当我们需要用户输入一长串信息 (比如 11 位手机号、地址、身份证号等等) 的时候，需要对这些信息进行分块处理，方便用户核对信息的正误。

注意事项

针对上述说的几个方面，我举两个反面案例来让大家直观感受一下。

注意点1：大量选项不进行分组的后果很严重

得亏这个菜单不是特别常用…否则如果频繁需要从这 29 个没有进行任何分组的项中选择自己想要的一两个，怕是会疯。

注意点2：描述词不清晰的后果也很严重

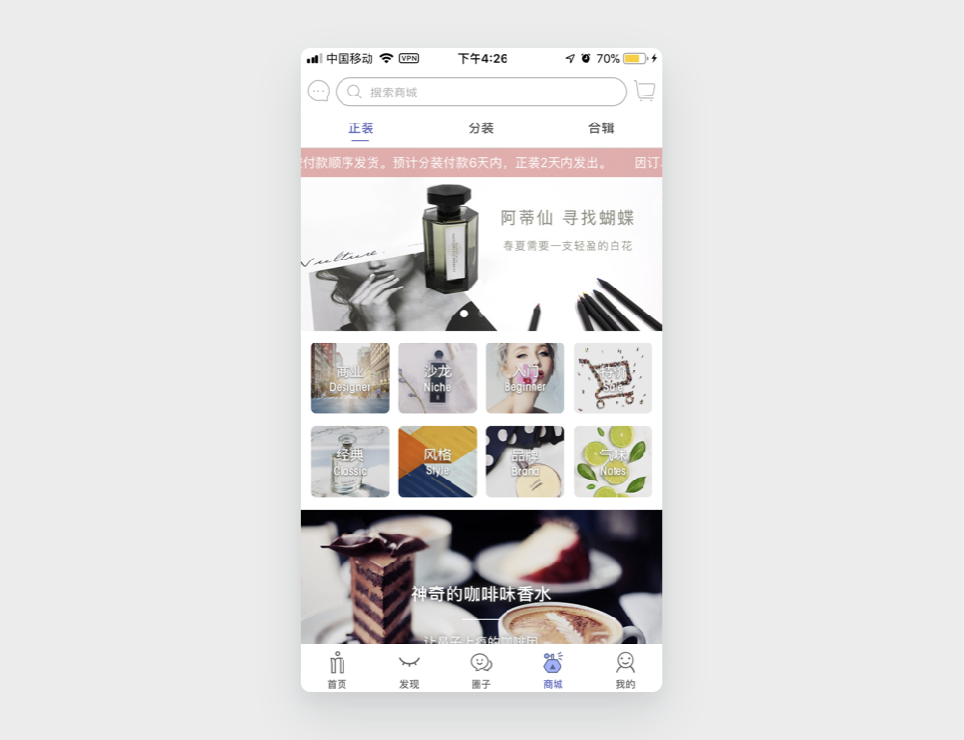
图片并不能表达选项本意的情况下，描述词还看不清楚，本来用户能够轻易理解和记忆这八个入口，现在只能记住四到五个，甚至更少。

总结

• 每一组选项从最多包含 7 (±2) 项；
• 选项较多时对选项进行分组，并尽可能使描述词清晰易懂；
• 长信息也需要分块处理；

参考

• George A. Miller. The Magical Number Seven, Plus or Minus Two: Some Limits on our Capacity for Processing Information. Psychological Review. 63 (2): 81–97.
• The Magical Number Seven, Plus or Minus Two — Wikipedia.
• 神奇的数字：7±2——维基百科中文